W dzisiejszym odcinku zajmiemy się przysłoną. Pokażę co oznaczają wartości wygrawerowane na pierścieniu przysłon (choć w dzisiejszych czasach raczej wartości wyświetlane na wyświetlaczu w wizjerze). I napiszę czego nie znaczą. Postaram się też pokazać dlaczego taki właśnie system jest użyteczny w fotografii i kiedy przestaje działać. Zapraszam.
Co to jest?
Tworzenie obrazu przez obiektyw polega na tym, że wszystkie promienie, które wpadają w niego zostaną skierowane w ten sam punkt na powierzchni matrycy, jeżeli tylko wychodzą z tego samego punktu na fotografowanym obiekcie. Przy fotografowaniu czegoś, co znajduje się w nieskończoności, oznacza to, że wszystkie promienie wpadające w obiektyw, które są do siebie nawzajem równoległe, spotkają się na matrycy w tym samym punkcie (a to, w którym punkcie, zależy od kierunku z jakiego wpadają w obiektyw). Od czego zależy zatem jasność obrazu na matrycy (oprócz jasności samego fotografowanego obiektu)? Od tego jak dużo równoległych do siebie promieni wpada w obiektyw. A od czego zależy ile ich wpadnie?
Jeżeli zajrzymy w obiektyw widzimy prześwit, który jest ograniczony zazwyczaj listkami przysłony (albo okrągłą ramką, w której są zamontowane). Oczywiście widzimy ten otwór przez część soczewek, z jakich obiektyw jest zrobiony, więc w rzeczywistości jest on innej wielkości niż nam się wydaje, gdy na niego patrzymy przez te soczewki. Ale to nie ważne. To co widzimy - obraz fizycznego otworu ograniczonego przez przysłonę widziany z zewnątrz (a nie prawdziwy otwór, taki, jakbyśmy go widzieli gdybyśmy wytłukli wszystkie soczewki) nazywa się źrenicą wejściową obiektywu. Jest ona o tyle ważna, że jeżeli jakiś promień biegnie tak, by się w niej zmieścić, to zostanie przez układ optyczny obiektywu tak załamany, że przejdzie przez rzeczywisty otwór przysłony i zostanie skupiony na filmie.
A więc jeżeli promienie biegnące równolegle są mniej więcej równomiernie rozłożone w przestrzeni (co jest prawdą jeżeli nie jest wyjątkowo ciemno), to ile ich wpadnie w obiektyw i zostanie skupionych na matrycy zależy od powierzchni źrenicy wejściowej. Jeżeli jej średnicę powiększymy
2 razy, to jego powierzchnia zwiększy się 2-krotnie, a więc obraz na matrycy stanie się jaśniejszy o "jedną działkę".
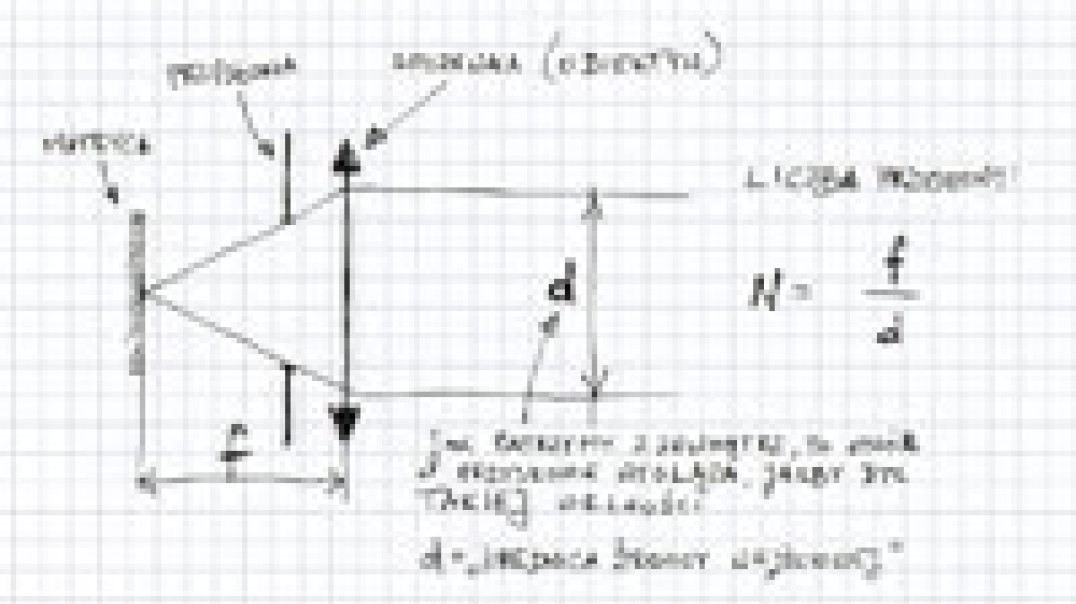
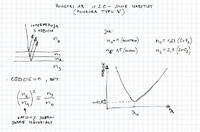
Jak to zależy od ogniskowej obiektywu? Załóżmy, że mamy jakiś obiektyw, tworzący na powierzchni matrycy jakiś obraz. Jeżeli teraz 2 razy przedłużymy ogniskową tego obiektywu zostawiając źrenicę wejściową taką samą jak była, to obraz na matrycy będzie 2 razy większy (czyli ten sam obraz będzie zajmował 4 razy większą powierzchnię). Ale będzie tworzony przez taką samą ilość promieni świetlnych. A skoro tak, to będzie 4 razy ciemniejszy, czyli o "dwie działki". Jeżeli chcemy, aby po przedłużeniu ogniskowej obraz nie stracił na jasności, musimy też powiększyć średnicę źrenicy wejściowej o dwie działki, czyli 2 razy. Jeszcze raz: jeżeli powiększasz ogniskową dwa razy, to średnicę źrenicy wejściowej obiektywu musisz też powiększyć 2 razy, aby obraz na matrycy był tak samo jasny. No to jak sobie podzielimy ogniskową przez średnicę źrenicy wejściowej, to dostaniemy liczbę, która przy określonej jasności fotografowanej sceny jednoznacznie nam określi, jak jasny będzie obraz na powierzchni matrycy. Przy założeniu, że obiektyw nie absorbuje światła, i że fotografujemy obiekt, który jest daleko (czyli odległość jest duża w porównaniu z ogniskową). Ta liczba to jest właśnie liczba przysłony. Oznaczamy to często f/liczba.
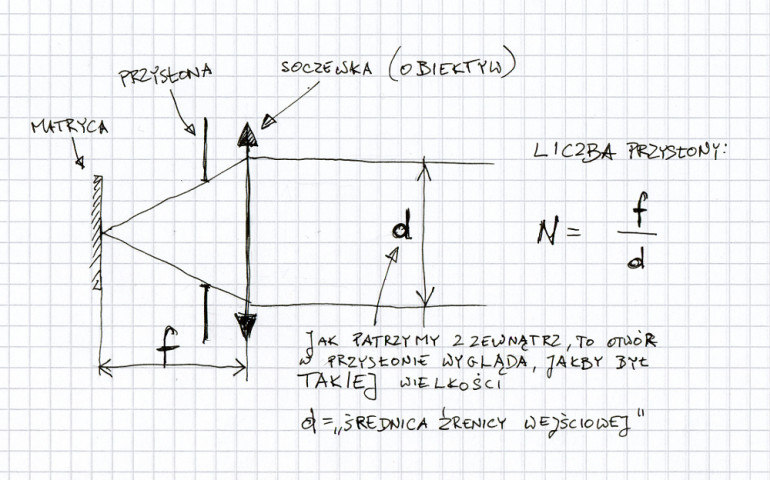
Jeżeli mamy obiektyw, który ma źrenicę wejściową o takiej samej średnicy, jak ogniskowa, to jego liczba przysłony wynosi 1. Przymykając o kolejne pełne działki zmniejszamy za każdym razem źrenicę wejściową
2 razy (zawsze w stosunku do ostatnio wyznaczonej wartości) i dostajemy ciąg f/1- f/1,4- f/2- f/2,8- f/4- f/5,6- f/8- f/11- f/16 itd. Jeżeli chcemy przymykać o pół działki, to zamiast
2 musimy przyjąć krok
2 i dostajemy mniej więcej: f/1- f/1,2- f/1,4- f/1,7- f/2- f/2,4- f/2,8- f/3,4- f/4... itd. Przymykając o jedną trzecią działki pierwiastek musi być 6 stopnia, czyli dostajemy: f/1- f/1,12- f/1,26- f/1,4- f/1,6- f/1,8- f/2- f/2,2- f/2,5- f/2,8- f/3,2- f/3,6- f/4- f/4,5- f/5- f/5,6... itd.
A jaśniej, się nie da?
Da się. Nie wiedzieć czemu ludzie podświadomie myślą, że f/1, to jest jakaś graniczna wartość, poniżej której się nie da. Już w 1961 roku pewna firma na C, produkująca dziś głównie kserokopiarki, drukarki komputerowe i troszkę aparatów fotograficznych, wypuściła na rynek obiektyw 50mm f/0,95. Dziś takie obiektywy pojawiają się czasem w świecie fotograficznym, choć bardziej popularne są w świecie kamer przemysłowych. I choć f/0,95 to tylko ok. 1/8 działki jaśniej, niż f/1.0 (czyli tyle, co nic) to na forach fotograficznych zdarzają się pytania w stylu "skoro f/1.0 przepuszcza do matrycy całe światło, jakie wpada w obiektyw, to znaczy, że f/0,95 przepuszcza więcej, niż wpuszcza?". I odpowiedzi w stylu "wyobrażam sobie, że to coś w rodzaju lejka". Otóż nie. Wprowadzając wcześniej liczbę przysłony nie zakładałem wcale żadnych strat światła wewnątrz obiektywu. Przeciwnie, założyłem, że obiektyw zawsze skupia na matrycy CAŁE światło, które w wpada w jego "prześwit". Zwiększanie jasności nie polega na przepuszczaniu coraz więcej, tego co wpadnie, tylko na powodowaniu, że coraz więcej wpadnie. Powiększając źrenicę wejściową co jedną działkę dostajemy kolejno wartości f/1-f/0,7-f/0,5-f/0,35 itd. Ograniczeniem teoretycznym jest f/0, choć taki obiektyw jest nieosiągalny, bo musiałby mieć nieskończenie wielką średnicę. Ale już dość dawno temu znana firma na Z produkowała do kamer kinematograficznych obiektyw 50mm f/0,7. f/0,7 to nie jest żaden lejek. To jest obiektyw o dwie "działki" jaśniejszy od f/1,4, który ma średnicę źrenicy wejściowej ok. 1,4 razy większą niż ogniskową. I tylko tyle to znaczy.
Czy jasne obiektywy muszą być duże?
Z liczbą przysłony wiążą się jeszcze aspekt rozmiarów, który robi się bolesny dla pleców, jeżeli chcemy robić zdjęcia z daleka. Jeżeli chcemy mieć obiektyw 50mm, o świetle 1.4, to znaczy, że źrenica wejściowa ma mieć średnicę ok. 3,5 cm. Czyli nic wielkiego. Jednak jeżeli taką jasność miałby mieć teleobiektyw 200mm to oznaczałoby to, że źrenica wejściowa ma mieć już ponad 14cm. I tu jest problem, bo choć można a nawet trzeba robić obiektywy, których przedni element jest większy od źrenicy wejściowej (na przykład w retrofokusach, czyli obiektywach szerokokątnych do lustrzanek), to zupełnie nie da się zrobić obiektywu, który miałby pierwszą soczewkę od źrenicy wejściowej mniejszą. Nawet jeżeli pozwolimy, aby obiektyw 200mm miał światło f/2.8 to średnica źrenicy wejściowej i tak wynosi 71mm co wymaga użycia gwintu na filtr 77mm (są firmy, które oferują takie obiektywy z gwintem 72mm, ale one po prostu troszeczkę "nie trzymają" jasności. Ale tylko troszeczkę, co praktycznego znaczenia nie ma). Efekt jest tego taki, że obiektywy długoogniskowe bardzo szybko robią się wręcz gigantyczne, a mimo to wcale nie są jasne.
Makro
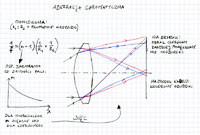
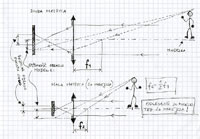
Wszystko to ładnie działa, dopóki fotografujemy coś, co jest daleko. Problem mogą mieć ludzie, którzy chcą fotografować na przykład pająki. A właściwie, to tacy ludzie mieli problem do lat 60. XX wieku, kiedy wymyślono światłomierze mierzące światło przez obiektyw. Problem polega na tym, że aby nastawić ostrość na coś, co jest blisko trzeba obiektyw oddalać od filmu. W miarę oddalania obiektywu od filmu obraz na matrycy powiększa się, a kąt widzenia się zawęża. W konsekwencji obraz staje się ciemniejszy. Gdyby ktoś mierzył światło zewnętrznym światłomierzem i ustawił czas i przysłonę tak, jak światłomierz każe, to by dostał zdjęcie niedoświetlone. Aby było dobrze, należy potraktować to, co podaje światłomierz, jako coś, co nazywa się efektywną liczbą przysłony. Żeby ustawić ostrość na coś, co jest blisko, ustawiamy obiektyw (który sobie sprowadziliśmy znowu do pojedynczej soczewki) o tak:
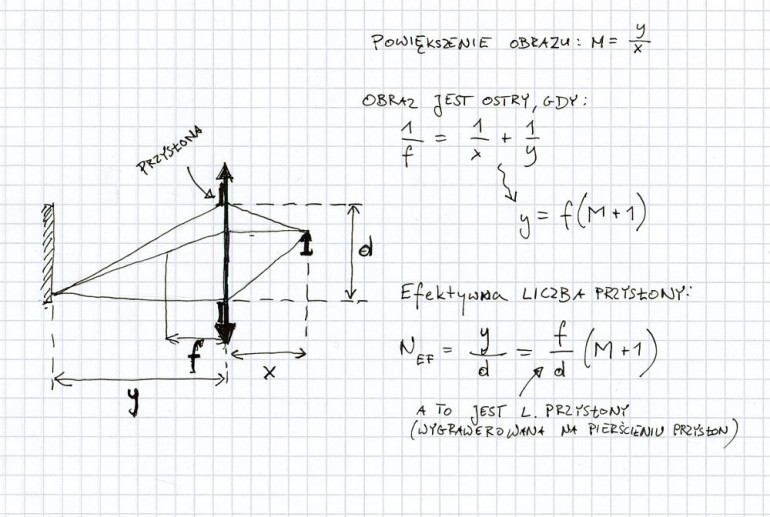
Efektywna liczba przysłony jest zdefiniowana podobnie do liczby przysłony, tylko to całą odległość obrazową (czyli to, co na rysunku jest ozn. y), a nie ogniskową obiektywu dzielimy przez średnicę źrenicy wejściowej. Jak sobie ktoś poprzekształca powyższe wzorki to mu wyjdzie, że aby uzyskać obraz M razy większy od samego przedmiotu trzeba ustawić soczewę w odległości y=(M+1)f od matrycy. I dostajemy: Efektywna liczba przysłony= (M+1) x liczba przysłony
Czyli jeżeli w makrofotografii używamy zewnętrznego światłomierza, to liczbę przysłony jaką podaje należy PODZIELIĆ przez M+1 i to ustawić na obiektywie. I będzie dobrze.
Przykład: jak chcemy uzyskać odwzorowanie 1:1 (czyli obraz ma być takich samych rozmiarów, jak przedmiot), to zarówno odległość przedmiotu do soczewki, jak soczewki od matrycy ma być równa dwóm ogniskowym. Jeżeli ustawimy przysłonę w aparacie np. na f/4, to efektywna liczba przysłony, jaką dostaniemy wyniesie f/8. Czyli o dwie działki ciemniej. Jeżeli zewnętrzny światłomierz nam mówi, że ma być f/4, to dla takiego odwzorowania musimy na obiektywie ustawić f/2.
A jak się używa pomiaru przez obiektyw, to światłomierz aparatu sam każe naświetlić na f/2, bo on mierzy bezpośrednio jasność obrazu w płaszczyźnie filmu.
Matryce
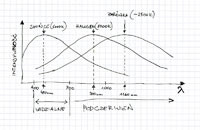
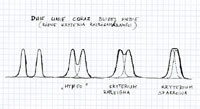
Okazuje się, że liczba przysłony czasem może nie do końca działać w przypadku lustrzanek cyfrowych. Ale tylko czasem. DxOMark opublikowało artykuł (o ten), w którym pisze, że matryce często nie są w stanie wykorzystać najjaśniejszych obiektywów przy całkiem otwartych przysłonach. Piszą, że jak się używa obiektywów przymkniętych, to działa, ale otwieranie ich do wartości np. f/1.4, czy f/1.2 nie powoduje, że matryca odbierze istotnie więcej.
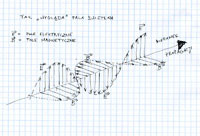
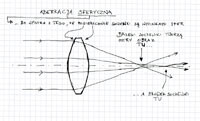
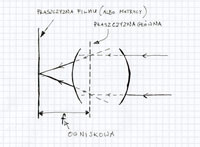
Ten fenomen jest dość prosty do wyjaśnienia, choć póki co to wyjaśnienie jest tylko hipotezą. Otóż w miarę otwierania przysłony powodujemy, że dodatkowe światło na konkretny piksel pada pod coraz większym kątem. Piksel natomiast ma na wierzchu mikrosoczewkę, która ma za zadanie kierować światło na tą jego część, która może absorbować fotony. Wygląda to jakoś tak:
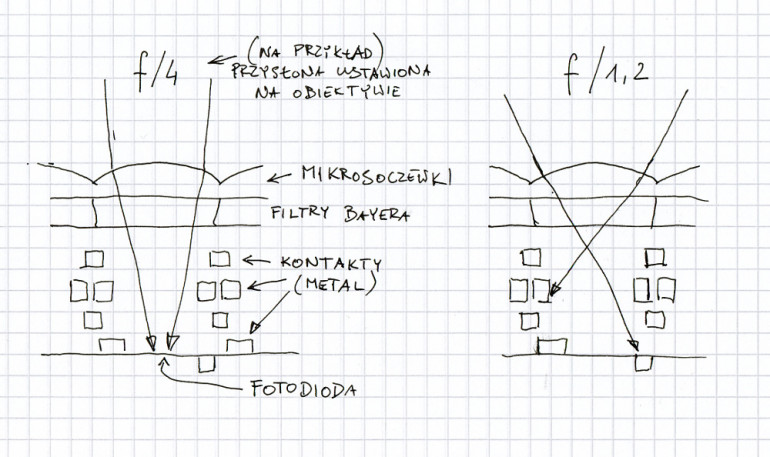
Jednym słowem taki piksel w matrycy stanowi układ optyczny, który również ma określoną jasność. I jeżeli promienie będą padały pod kątem zbyt dalekim od prostopadłego, to się okazuje, że mikrosoczewka może tracić wydajność i coraz większa część światła pada na kontakty bramek, a nie na samą aktywną część pikseli.
A w następnym odcinku będzie o tym skąd się bierze głębia ostrości